投稿日:

仕事算

2014年慶應湘南の6番です。

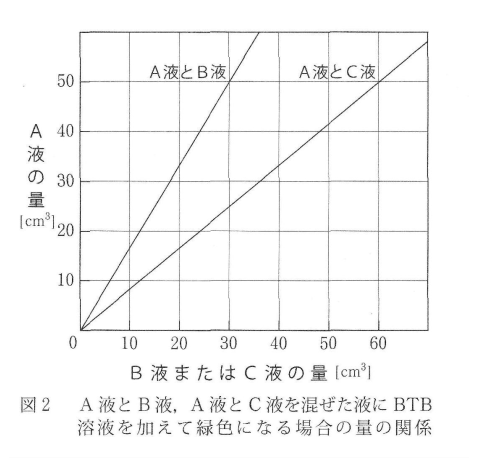
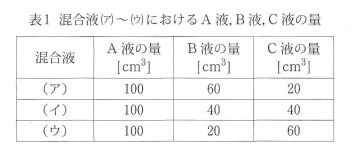
ある工事現場に3本のクレーンA、B、Cがある。3本のクレーンをすべて使うとちょうど8日間で、BとCの2本のクレーンだけを使うとちょうど12日間で、Cのクレーンだけを使うとちょうど36日間でそれぞれ全体の作業を終わらせることができる。工事は毎日行うものとして、次の問いに答えなさい。
（1）クレーンAだけを使うと、作業を始めてから何日目で全体の作業を終わらせることができますか。
（2）クレーンAだけをちょうど5日間使い、残りをクレーンBとクレーンCの2本だけを使って作業をした。作業を始めてから何日目で全体の作業を終わらせることができますか。
（3）A、B、Cのクレーンから1日ごとにどれか1本だけを選んで作業をしたところ、全部でちょうど21日間で全体の作業を終わらせることができた。Bを使用した日数がAを使用した日数の2倍であったとき、Bを使用した日数は何日ですか。

(1) 8日、12日、36日とあるので、全体の仕事を【72】と考えてみると
A＋B＋C＝【72】÷8＝【9】
B＋C＝【72】÷12＝【6】
C＝【72】÷36＝【2】
です。
Aは【9】－【6】＝【3】ですから、【72】÷【3】＝24日間です。

【答え】24日

（2）
【3】×5＝【15】ですから、残りの仕事は【72】－【15】＝【57】
【57】÷【6】＝9･･･【3】ですから10日なので5日＋10日＝15日

【答え】15日

（3）A、B、Cが使われた日数をそれぞれA、B、Cとすると
A＋B＋C＝21･･･ア
B＝A×2･･･イ
【3】×A＋【4】×B＋【2】×C＝【72】･･･ウ

ということになります。
イをアに入れると、A×3＋C＝21･･･エ

イをウにいれると
【3】×A＋【4】×2×A＋【2】×C＝【11】×A＋【2】×C＝【72】･･･オ

エから
【6】×A＋【2】×C＝【42】･･･カ

オとカの差から【5】×A＝【30】　A＝6日
したがってAは6×2＝12日になります。

【答え】12日

やはり例年の6番と比してやさしかったでしょう。今年は昨日解説した5番もそれほど難しくはなかったので、平均点は確実に高かったと思います。これが来年も続くのかどうか、はわかりませんが、問題がやさしくなった分、明らかにミスはかなり厳しい結果をもたらすことになるので、より一層ていねいに解く練習をしていかなければなりません。

受験で子どもと普通に幸せになる方法、本日の記事は
もう一度やることを整理する

今日の田中貴.com
生活のペースを崩さない

5年生の教室から
動機付け

冬期講習のお知らせ

慶應進学オンライン


投稿日:

中和に関する問題

2014年慶應中等部の問題です。

ある濃度の水酸化ナトリウム水溶液をA液とし、たがいに濃度の異なる塩酸をそれぞれB液とC液とします。A液とB液、または、A液とC液を混ぜて、BTB溶液を加えたときに、緑色になる場合のそれぞれの体積の関係を表すと図2のグラフのようになりました。あとの問いに答えなさい。

（1）B液とC液の濃度の関係について正しいものを次の中から選びなさい。

　　1　C液よりB液の方が濃度が高い。
　　2　B液よりC液の方が濃度が高い。

（2）A液とB液とC液の量を表1の組み合わせにした混合液（ア）～（ウ）にそれぞれBTB溶液を加えると、何色になりますか。次の中から選びなさい。

　1赤色　　2　青色　　3　黄色　　4　緑色

（3）A液60cm3にB液を加え、加熱して残った固体の重さを調べました。加えたB液の量と残った固体の重さの関係を表すと、次のどのグラフのようになりますか。

（4）（3）のグラフの中の○に当てはまる値はいくらになりますか。二けたの整数で答えなさい。

（5）B液45cm3にA液を加え、加熱して残った固体の重さを調べました。加えたA液の量と残った固体の重さの関係を表すと、次のどのグラフのようになりますか

（6）（5）のグラフの中の口に当てはまる値はいくらになりますか。二けたの整数で答えなさい。

（7）B液30cm3に、次の（ア）～（エ）の体積のA液を加えた液を加熱しました。それぞれの場合に残る固体は何ですか。あとの1～4の中から選びなさい。

　　（ア）Ocm3　（イ）20cm3　（ウ）40cm3　（エ）60cm3

　1 何も残らない　　2　食塩　　3　水酸化ナトリウム　　4　食塩と水酸化ナトリウム

（8）A液とC液の混合液を次の（ア）～（ウ）の体積の組み合わせで作り、そこに鉄片とアルミニウム片を入れました。このときの鉄片とアルミニウム片の様子について正しいものはどれですか。

（ア）～（ウ）のそれぞれについて、あとの1～4の中から選びなさい。

（ア）A液50cm3、C液60cm3
（イ）A液80cm3、C液20cm3
（ウ）A液30cm3、C液100cm3
　　　　　　　　　
1　鉄片だけから泡が出る。
2　アルミニウム片だけから泡が出る。
3　鉄片とアルミニウム片の両方から泡が出る。
4　鉄片とアルミニウム片の両方とも泡は出ない。

（9）（8）で泡が出ている場合、その泡は何という物質ですか。次の中から選びなさい。

　1　アンモニア　　　2　酸素　　　3　水素　　　4　ちっ素　　　5　二酸化炭素

(解説と解答）
（1）C液の方が中和するのに多くの量を使っているので、Cの方がうすいことがわかります。BはCの2倍の濃さになっています。
【答え】1

（2）（ア）はAとBで中和してしまうので、Cを入れると酸性になります。
（イ）Cを40㎝3入れるということはBを20㎝3入れると同じになるのでちょうどBが60cm3になるから、中和します。
（ウ）C60cm3はB30cm3ですから、Bを50㎝3入れることと同じなので、足りませんからアルカリ性になります。

【答え】（ア）3　（イ）4　（ウ）2

（3）水酸化ナトリウム水溶液を固定するので、最初が0ではなく、中和した後固体の量は変わりません。
【答え】4

（4）Aが60cm3ですから、A：B＝5：3で中和するので、60÷5×3＝36cm3です。
【答え】十の位　3　　一の位　6

（5）今度は塩酸を固定するので、グラフは0から始まり、その後変化量が減りますが、増え続けます。
【答え】2

（6）B液が45cm3ですから、45÷3×5＝75cm3です。
【答え】十の位　7　位置の位　5

（7）B30cm3と中和するのは、30÷3×5＝50㎝3のA液です。
塩酸を固定しているのでアの場合は何も残りません。イの場合がすべてが食塩になります。
ウの場合もすべて食塩になります。エの場合は塩酸がなくなるので、水酸化ナトリウムも残ります。
【答え】（ア）1　（イ）2　（ウ）2　（エ）4

（8）（ア）の場合はちょうど中和しますから、両方とも泡は出ません。
（イ）の場合は水酸化ナトリウム水溶液が残るので、アルミニウムだけが反応します。
（ウ）の場合は塩酸が残るので、鉄もアルミニウムも反応します。
【答え】（ア）4　（イ）2　（ウ）3

（9）出てくる気体は水素です。
【答え】3

受験で子どもと普通に幸せになる方法、本日の記事は
正月特訓

5年生の教室から
志望校がコロコロ変わる

今日の田中貴.com
新しいものはもう買わない

冬期講習のお知らせ

慶應進学オンライン


投稿日:

消去算

2015年湘南の問題です。

バスを1台借りて遊園地へ行く。1人あたりの参加費用は、遊園地の入場料とバスの1人あたりの代金を合わせた金額である。遊園地の大人1人あたりの入場料は、小学生1人あたりの入場料の1.5倍である。バスの1人あたりの代金は、バス1台分の料金を参加人数で割った金額（1円未満は切り上げ）で、大人も小学生も等しく支払う。
大人9人と小学生15人が参加すれば、大人1人あたりの参加費用は7800円になり、大人10人と小学生20人が参加すれば、小学生1人あたりの参加費用は6000円になるという。大人1人あたりの入場料はいくらですか。

【解説と解答】
子どもの料金を【2】とすると、大人の料金は【3】。
またバスの料金は24と30の公倍数が便利なので、＜120＞とします。
すると大人9人、小学生15人の場合、大人の参加費は＜5＞＋【3】＝7800･･･ア
大人10人、小学生20人の場合の小学生の参加火は＜4＞＋【2】＝6000･･･イ

ア×2　＜10＞＋【6】＝15600
イ×3　＜12＞＋【6】＝18000　より＜2＞＝2400　＜1＞＝1200　
7800－1200×5＝1800円が大人の入場料です。
（答え）1800円

冬期講習のお知らせ

受験で子どもと普通に幸せになる方法、本日の記事は
できる子ができなくなる？

5年生の教室から
できない時こそがんばれ

今日の田中貴.com
偏差値はふわっととらえる

新6年生を募集中です。

慶應進学オンライン


投稿日:

水に関する問題

2010年　慶應湘南の問題

以下のような実験をしました。次の問いに答えなさい。
［実験1］
　水をビーカーに入れ、ガスバーナーで熱し、そのときの水のよう
すを観察した。

［実験2］
　透明なガラスのコップに水を入れ、図1のように水面の位置がわかるように線を書いた。このコップを冷凍庫でしばらく冷やし、できた氷のようすを観察した。

　［実験3］
　水が入っているガラスのコップの中にドライアイスを入れ、そのようすを観察した。

（問1）［実験1］において、しばらく熱すると水の中から、あわが次々と出てきました。このあわはどんな気体によるものですか。出てきた量が最も多い気体を次の中から1つ選び、記号で答えなさい。

　1　空気　　2　酸素　　3　水素　　4　水蒸気　　5　二酸化炭素

（問2）（問1）の気体を確認するときに使うもの、およびその変化のようすとして正しいものを、次の中から1つずつ選び、それぞれ番号で答えなさい。

（使うもの）
1　赤色リトマス紙　　2　青色リトマス紙　　3　塩化コバルト紙
4　気体検知管　　　　5　マッチ　　　　　　6　石灰水
（変化のようす）

1　赤色になる　2　青色になる　　　　3　黄色になる
4　白くにごる　5　火が消える　　　　6　ボンと吉を出して燃える

（問3）［実験1］において、しばらく熱すると水の表面から湯気が上がっていることが観察できました。この湯気ができるしくみを、40字以内で説明しなさい。

（問4）［実験2］において、水が氷になったときのようすとして、正しいものを次の中から1つ選び、番号で答えなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
（問5）［実験3］において、しばらくするとコップから白い煙のようなものが出てきました。この白い煙のようなもののでき方として、正しいものを次の中から1つ選び、番号で答えなさい。

1　ドライアイスから出てきた二酸化炭素が、空気によって冷やされてできた。

2　ドライアイスから出てきた二酸化炭素が、水によって冷やされてできた。

3　ドライアイスから出てきた二酸化炭素が、ドライアイスによって冷やされてできた。

4　空気中の水蒸気が、ドライアイスから出てきた二酸化炭素によって冷やされてできた。
　　　　　　　　　　　　
5　ドライアイスによって冷やされた水が、沸騰してできた。

（解答）
問１　ここでは出てきた量が一番多いものとなっていますので、そうなると水蒸気になるでしょう。空気も交じっていますが、水蒸気の量よりは少なくなります。　（答え）４

問２　
水があるかどうかを感知するものが、塩化コバルト紙です。ふつうは青く、湿気があると赤く変化します。

（答え）使うもの　３　変化のようす　１

問３　湯気は実際には水です。これを水蒸気と思っている子は案外少なくありません。水蒸気は目に見えない。これはしっかり覚えておきましょう。

（答え）　水面から蒸発した水蒸気が冷やされて細かな水滴となっている。

問４　水が氷になれば膨張しますが、この場合真ん中が膨らみます。
（答え）３

問５　これも原理的には問３と同じですが、水蒸気が冷やされて白い煙のように見えるのです。
（答え）４

原理的には簡単な問題ではありますが、湘南ではよく出題されるので、しっかり基本をマスターしておきましょう。

冬期講習のお知らせ

受験で子どもと普通に幸せになる方法、本日の記事は
過去問ができない？

5年生の教室から
もう受験に疲れた？

今日の田中貴.com
電気に関する問題

新6年生を募集中です。

慶應進学オンライン


投稿日:

規則性に関する問題

2013年慶應湘南の問題です。

図１のようにならんでいる分数の書かれた黒タイルと白タイルを、図２のようにならべかえる。（　　　）にあてはまる数を答えなさい。

（１）12段目のタイルに書かれた分数の和は（　　　）である。

（２）1段目から（　　）段目までのタイルに書かれた分数の和は76 1/2である。

（２）黒いタイルを576枚ならべたとき、すべての黒いタイルに書かれた分数の和は（　　　　）である。

（１）12段目は分母が13になるので、分子は1から12までになります。
1から12までの和は（1＋12）×12÷2＝78ですから　和は78÷13＝6　になります。
（答え）6

（２）1段目が0.5　2段目が1、3段目が1.5と0.5ずつ増えています。
ｎ段目は0.5＋0.5×（ｎ－1）になるので、和は
（0.5＋0.5×ｎ）×ｎ÷2＝76.5より（ｎ＋1）×ｎ＝306＝17×18より17段目
（答え）17段目

（３）黒いタイルは分母が偶数です。
したがって、１＋3＋5＋…と枚数は奇数の和になりますが、奇数の和は平方数になるので、
576＝24×24から24番目、すなわち2×24－1＝47ですから分母が48までを足したことがわかります。
48段目は（1＋47）×47÷2÷48＝23.5が和ですから
（0.5＋23.5）×24÷2＝288
（答え）288

（２）の式の変形で、素因数分解に持ち込まなければいけないところが、解法の分かれ目になっていたと思います。

今日の田中貴.com
先生がいない

受験で子どもと普通に幸せになる方法、本日の記事は
どこがわからないか、わからない

5年生の教室から
5年生の秋に第一志望を決める（4）ー子どもの意志ー

慶應進学オンライン


投稿日:

流水算

2013年の慶應湘南の問題です。流水算は割と出題される傾向が高いのですが、問題はそう単純ではありません。
以下に条件を整理するか、がポイントになるでしょう。

分速40mで流れる川に船着き場Kがあり、その下流に船着き場0がある。いま、Kには静水時に分速160mで進む船Aと、分速260mで進む船Bがある。船AはKを0に向けて出発し、26分後にうきわⅩを船から川に流し、その数分後、うきわYを川に流した。船Bは船Aが出発してから65分後にKを0に向けて出発し、その数分後、うきわⅩを拾った。船Aは0に到着後すぐに向きを変えて再びKに向けて出発したところ、25分後に船Bと会い、さらにその15分後にうきわYを拾った。
（1）船BがうきわⅩを拾ったのは、船Bが出発してから何分後ですか。
（2）KO間の距離は何kmですか。
（3）船AがうきわYを川に流したのは、うきわⅩを川に流してから何分後ですか。

(解説）
（１）Aは分速200mで下ります。25分後ですからKから200×26＝5200mのところでうきわXを流しました。船Bが出るとき、流され始めて39分たっていますから、うきわXはKから5200＋40×39＝6760mのところにあります。
6760÷260＝26
（答え）26分後

（２）Aは上りは160－40＝120mの分速です。AがOに着いて、すぐ折り返し25分後にBをあったので、AがKに着いたとき、AとBの間の距離は（300＋120）×25＝10500ｍ
離れていました。BがKを出発したときには200×65＝13000m離れていたので
13000－10500＝2500m差が縮まったことになります。AとBの差は100mなので
2500÷100＝25分がBが出発してからAがOに到着するまでの時間になるので、Aは
25＋65＝90分KからOまでかかっていますから200×90＝18000m＝18km
（答え）18km

（３）AがうきわYを拾ったのはOを出発してから40分後なのでOから
120×40＝4800mのところです。
AがOに着いたときはその40分前ですから、その時、うきわYは40×40＝1600mさらに上流にいました。したがってAがOについたとき、うきわYはOの上流
1600＋4800＝6400mのところにいたことがわかります。
落としたところから毎分160mの差がついているので6400÷160＝40分ですから、AがうきわYを落としたのはO到着の40分前。したがって90－40＝50分でKを出発してから50分後になります。50－26＝24分後
（答え）24分後

今日の田中貴.com
ミスはするものだという前提で考える

受験で子どもと普通に幸せになる方法、本日の記事は
9月の成績が悪くても気に病むな

5年生の教室から
ノートの違い

慶應進学オンライン


投稿日:

平面図形の問題

2014年　慶應普通部の９番です。

下の図のような三角形ABCがあり、辺AB、BCをそれぞれ3等分した点をD、E、F、Gとします。また、辺ACの真ん中の点をHとします。
ア、イ、ウの面積の合計とエの免責との差は、三角形ABCの面積の何倍ですか。

何となく補助線を引きたくなる問題ではあるのですが、面積の差と言っているので、同じものを足したり、引いたりすることで解けるのではないだろうか、という感じがします。

そこで、ちょっと書いてみましょう。

三角形ABF＝ア＋キ＋ウ＝$$frac{1}{3}$$

三角形BHC＝ア＋オ＋イ＝$$frac{1}{2}$$

三角形ADC＝イ＋カ＋ウ＝$$frac{1}{3}$$

これを全部加えると
ア＋ア＋イ＋イ＋ウ＋ウ＋キ＋オ＋カ＝$$frac{7}{6}$$

全体は
ア＋イ＋ウ＋エ＋オ＋カ＋キ＝1ですから、これを引くと

ア＋イ＋ウ－エ＝$$frac{1}{6}$$となります。

【答え】$$frac{1}{6}$$

今日の田中貴.com

雲の問題

受験で子どもと普通に幸せになる方法、本日の記事は

練習して覚えなさい、ただそれだけです。

慶應進学オンライン


投稿日:

やりとりに関する問題

2013年の普通部です。

順に条件を追っていけば良いだけですが、案外ミスがでやすい問題です。

A、B、Cの箱におはじきがそれぞれ何個か入っています。まずAからCへ8個移すと、AとBの個数の和がCの個数と等しくなりました。次にBからCへ6個移すと、Aの個数はCの個数の4割となりました。最後にAからBへ8個移すと、Bの個数はCの個数の半分となりました。はじめAに何個のおはじきが入っていましたか。

全体の個数は変わっていないので最初AからCに8個移動したとき、全体を【2】とするとCは【1】、A＋B＝【1】です。

次にBからCに6個移したとき、Cは【1】＋6ですから最後にBは【0.5】＋3

A＋B＝【1】のときにBは【0.5】＋3－8＋6＝【0.5】＋1　

するとAは【0.5】－1 になるので

【1】＋6：【0.5】－1＝5：2　となります。内項の積＝外項の積より

【2.5】－5＝【2】＋12　【0.5】＝17

【1】＝34　と求められるので、

Aは34×0.5－1＋8＝17＋7＝24

（答え）24個

こういう問題は確実に得点したいところです。

=============================================================
今日の田中貴.com

第237回　カリキュラムの罠
==============================================================
受験で子どもと普通に幸せになる方法、本日の記事は

式が書ける子は伸びる
==============================================================

==============================================================
慶應進学オンライン
==============================================================

==============================================================

==============================================================


投稿日:

展開図に関する問題

2014年普通部算数5番です。

同じ大きさの正三角形を8枚あわせて、図1のような立体をつくりました。図2はこの立体の展開図です。

(1)　図2の太線は、図1の立体のどの辺ですか。
(2)　立体の8つの面に1から8の数字を1つずつ書き、サイコロのように向かい合う面の数字の和が等しくなるようにしました。図2のア～エの面に書かれている数字を答えなさい。

（１）
展開図について、それぞれの頂点に記号を入れていくと以下の通りになります。

記号の入れ方としては6の三角形の右下の頂点がCと決まります。（６が表になるので、ABは左側の斜辺と決まりますから、右下はCです。）
するとアと書かれている三角形の右上はDと決まり、１のかかれている三角形の左上の頂点はAですから、下の頂点はEと決まります。
5の書かれた三角形の左下はまたAとなり、その右下の点はDと決まります。

したがって太線は辺ADです。

（答え）辺AD

（２）
1から8までの和は（1＋8）×8÷2＝36で、面は8面ですから2面ずつの組み合わせとしては4組あるので36÷4＝9です。
したがって和が9になるようにすればいいので、上図のように入りますから、
アは7　イは4　ウは3　エは8です。

（答え）
ア　7　イ　4　ウ　3　エ　8

=============================================================
今日の田中貴.com

量をやる、ということの誤解
==============================================================
受験で子どもと普通に幸せになる方法、本日の記事は

問題が読めていない
==============================================================

==============================================================
慶應進学オンライン
==============================================================

==============================================================

==============================================================